化学、新課程の一番大きな変更点である熱化学の範囲がどう変わったのかをみていきます。
新課程では従来の熱化学方程式を用いた表記をやめ、反応エンタルピーを用いた表記を行うようになりました。ネットなどでは、反応熱と反応エンタルピーは符号が逆になる‥‥それだけだ、といった説明もあるのですが、さすがにそれだけではありません。いろいろなところに影響が出てきます。
この辺り、どのような影響が出るのかを、旧課程履修者の目線から解説します。このページの解説に問題演習を追加した電子書籍を作成、販売しています。活用ください。(Kindleストアへ)
はじめに
2025年度から新課程に対応した入試が始まります。化学でも用語の変更や学習順序の変更などが行われています。それらのうちで最も大きく変更されたのが「化学反応とエネルギー」の範囲です。
「化学反応とエネルギー」の範囲では,以前より用いられていた熱化学方程式が廃止され,エンタルピーを用いた表記に変更されています。
(旧)熱化学方程式 C(固) + O2(気) = CO2(気) + 394kJ
(新)エンタルピー変化を付した反応式
C(固) + O2(気) → CO2(気) ,ΔH=-394kJ
このような表記になります。
化学反応式に状態を添えて書き,その横に反応エンタルピーを書き添えます。\(\Delta H\)はエンタルピーの変化量なのですが,このエンタルピーとは何か,なぜ符号が代わっているのかなどを説明するのが本書の目的になります。
2025年度入試では,旧課程履修者への配慮が行われますが,だからといって新課程の知識は必要なしとはいかないでしょう。エンタルピーを用いた新しい表記を学んでいきましょう。
化学反応とエネルギーのおさらい
まずは旧課程での表記,用語などをおさらいしておきましょう。新課程履修者も,過去問題を解くことを考えればこれらの知識が必要になると思われます。既学習者の復習を兼ねて旧課程での学習内容を簡単に説明します。
熱化学方程式(旧課程)
仕事をする能力を数値として表したものをエネルギーといいます。物が燃えると熱などのエネルギーが発生しますがこのような化学反応に伴う熱の出入りを表すために用いられる化学反応式の一種が熱化学方程式でした。熱が発生する反応を発熱反応,熱を吸収する反応を吸熱反応といい,それぞれ+とーを用いて次のように表していました。
熱化学方程式 2H2(気) + O2(気) = 2H2O(液) + 286kJ
2C(黒鉛) + 2H2(気) = C2H4(気) – 52.5kJ
化学反応熱の種類(旧課程)
ある生成物1molを構成元素の単体から合成する際に発生する熱を生成熱,ある物質1molが完全燃焼する際に発生する熱を燃焼熱といいます。他にも物質1molが融解するのに必要な熱を融解熱,気化するのに必要な熱を気化熱などと呼びました。新課程ではこれらの用語は生成エンタルピーなどに変更されています。
ヘスの法則(旧課程)
化学反応で生成物と反応物が同じならば,反応の種類や経路によらず,その反応熱は等しくなります。これをヘスの法則といいます。ヘスの法則を用いると,いくつかの熱化学方程式から未知の反応熱を計算によって求めることができます。例えばメタノールの燃焼熱は,メタノール・二酸化炭素・水(液体)の生成熱を用いて次のように求める事ができます。
C(黒鉛) + 2H2(気) + \(\frac 12\)O2(気) = CH3OH(液) + 239kJ ‥‥‥①
C(黒鉛) + O2(気) = CO2(気) + 394kJ ‥‥‥②
H2(気) + \(\frac 12\)O2(気) = H2O(液) + 286kJ ‥‥‥③
(②式) – (①式) + (③式 × 2)と計算すると
CH3OH(気) + \(\frac 32\)O2(気) = CO2(気) + 2H2O(液) + 727kJ ‥‥‥④
このように,旧課程では①~③の熱化学方程式を連立方程式のように扱い,④の熱化学方程式を求めていました。このようなことが可能であったのは,反応物質や生成物質の持っている化学エネルギーの総和が決まっているからで,最初と最後のエネルギーが決まっていればどのような経路を通ったとしてもエネルギーの出し入れは変わらないからと説明されました。
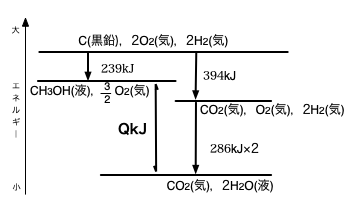
これらの考え方は新課程でも原則的には変わりません。厳密には違いますが,今は反応物質の持っている化学エネルギーの和の呼び方が「エンタルピー」と変わったと思っておいてください(正確には違いますがひとまずそう思っておいてください)。
化学反応と反応エンタルピー
ここから,反応エンタルピーについて詳しく見ていきます。本書の目的は新課程での変更点を知ることなので旧課程と比較しながら説明します。反応エンタルピー
メタノール生成の反応を熱化学方程式を用いて表すと
C(黒鉛) + 2H2(気) + \(\frac 12\)O2(気) = CH3OH(液) + 239kJ ‥‥‥①
となります。これをエネルギー図を用いて表すと
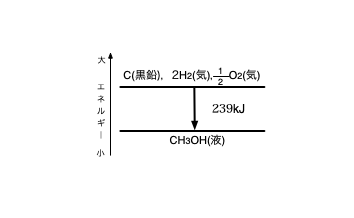
となり,反応物質のエネルギーの総和《C(黒鉛) + 2H2(気) + \(\frac 12\)O2(気)》と生成物質のエネルギーの総和《CH3OH(液)》の差が熱エネルギー《239kJ》となって放出された発熱反応と説明されます。
これに対し①の熱化学方程式をエンタルピー変化を付した化学反応式で表すと次のようになります。
C(黒鉛) + 2H2(気) + \(\frac 12\)O2(気) → CH3OH(液) ΔH=-239kJ ‥‥‥①’
エンタルピーは物質の持つ内部エネルギーを表す値です(正確には違いますが,高校の学習内容に従う限りはこのように考えて問題ないです)。①’の式で生成物質のエンタルピーの総和《CH3OH(液)》から反応物質のエンタルピーの総和《C(黒鉛) + 2H2(気) + \(\frac 12\)O2(気)》を引いた,エンタルピーの変化量がΔHに相当します。
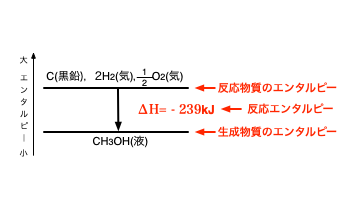
ΔHはエンタルピーの変化なので生成物質のエンタルピーの総和から反応物質のエンタルピーの総和を引くことに注意してください
生成物質のエンタルピーの総和反応物質のエンタルピーの総和
化学反応によってエンタルピーの総和が減少したので\(\Delta H < 0\)であり,減少したエンタルピーに応じて熱エネルギーが放出されるので+239kJの発熱反応となった‥‥ということになります。反応エンタルピーはエンタルピーの変化量,反応熱は外部に放出される熱エネルギー。なので両者は大きさが等しく符号が異なる値になります。
エンタルピー変化とエネルギー変化
エンタルピーの変化量とエネルギーの変化量は厳密には異なっています。これは物質が膨張する際に仕事をするからで,反応によって放出されるエネルギーをQ,膨張によって行われる仕事をW,物質の内部エネルギーの変化をΔUと表すと
$$\Delta U + Q +W =0$$
の関係が成り立ちます。定圧下では\(\Delta H = -Q \)の関係が成り立つので,ここに上式を代入し$$\Delta H = -Q =\Delta U + W \neq \Delta U$$
が成立します。
[発展]エンタルピーHは次のように定義されます
$$H=U+PV$$
ここでは内部エネルギーでは圧力と体積の積になります。このように定義するとが成立するため,定圧下での反応熱を議論しやすくなります。定圧下での反応熱を議論し易くするために導入された,内部エネルギーに相当するもの……という理解をしておいてください。
ヘスの法則
新課程の表現を用いてヘスの法則について,あらためて説明します。
化学反応で物質の最初の状態と最後の状態が決まっていれば,途中の反応経路によらず反応エンタルピーの総和は一定となります。これをヘスの法則と言います。ヘスの法則を用いると,いくつかの反応エンタルピーを付した化学反応式(熱化学反応式という表現もあります)から未知の反応エンタルピーを計算によって求めることができます。例えばメタノールの燃焼反応の反応エンタルピーを,下のメタノール・二酸化炭素・水(液体)が生成する熱化学反応式を用いて求めてみます。
C(黒鉛) + 2H2(気) + \(\frac 12\)O2(気) → CH3OH(液) \(\Delta H_1 = -239kJ\)‥‥‥①
C(黒鉛) + O2(気) → CO2(気) \(\Delta H_2 = -394kJ\)‥‥‥②
H2(気) + \(\frac 12\)O2(気) → H2O(液) \(\Delta H_3 = -286kJ\)‥‥‥③
(②式) – (①式) + (③式 × 2)と化学反応式を足し合わせると
CH3OH(気) + \(\frac 32\)O2(気) → CO2(気) + 2H2O(液) ‥‥‥④
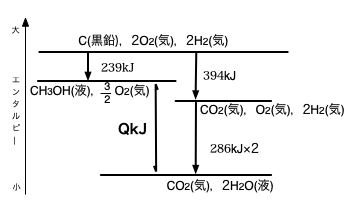
熱化学方程式のときと同じように,複数の熱化学反応式を加減することで目的の化学反応式を作ります。④の反応の反応エンタルピーは
$$\Delta H = \Delta H_2 – \Delta H_1 + \Delta H_3 \times 2 = -394 – (239)+(-286) \times 2 = -727kJ$$
と計算され,反応エンタルピーを付記した化学反応式は
CH3OH(気) + \(\frac 32\)O2(気) → CO2(気) + 2H2O(液) \(\Delta H = -727kJ\) ‥‥‥④’
と求められます。
反応エンタルピーの種類
化学反応の種類に応じて以下のような反応エンタルピーが存在します。
生成エンタルピー
ある生成物1molを構成元素の単体から合成する際の反応エンタルピーです。単体は化合物より不安定(高エネルギー)な事が多いため負の値を取る事が多くなります。反応エンタルピーを付した化学反応式は次のようになり
C(黒鉛) + 2H2(気) + O2(気) → CH3OH(液) \(\Delta H = -239kJ\)
メタノールの生成エンタルピーは\(\Delta H = -239kJ\)となります。
分解エンタルピー
ある化合物1molから構成元素の単体へ分解する際の反応エンタルピーです。
燃焼エンタルピー
ある物質1molが完全燃焼する際の反応エンタルピーです。完全燃焼した後に生じる酸化物は,炭素なら二酸化炭素というように決まっているので覚えてください。
状態変化の反応エンタルピー
物質1molが融解する際の反応エンタルピーを融解エンタルピーといいます。氷の融解は
H2O(固) → H2O(液) \(\Delta H = 6.0kJ\)
と表され,融解エンタルピーは6.0kJ/molとなります。ここで水の凝固は
H2O(液) → H2O(固) \(\Delta H = -6.0kJ\)
と表され,水の凝固エンタルピーは-6.0kJ/molになることに注意しなければいけません。また,氷の融解熱および水の凝固熱はいずれも6.0kJ/molであり,吸熱反応の場合でも-6.0kJ/molとはせず,絶対値を取った値で答えます。
気化エンタルピー・凝縮エンタルピー・昇華エンタルピーなど,そのほかの状態変化の反応エンタルピーも同様に定義されます。
中和エンタルピー
1molの水素イオン\(H^+\)と水酸化物イオン\(OH^-\)が反応するときの反応エンタルピーです。薄い強酸と強塩基の水溶液の場合の中和エンタルピーは\(-56.5kJ/mol\)となります。
$$H^+aq + OH^-aq → H_2O(液) \quad \Delta H = -56.5kJ$$
酸と塩基の種類により少し値が異なるので注意してください。
溶解エンタルピー
溶質が溶媒に溶解する際の反応エンタルピーです。
エネルギーの分類
結合エネルギー
1molの結合を切断するのに必要なエネルギーです。
解離エネルギー
分子1molを構成元素まで分解するのに必要なエネルギーです。
格子エネルギー
1molの結晶の構成元素すべてを原子まで分解するのに必要なエネルギーです。
活性化エネルギー
反応物を1molの遷移状態(活性化状態)にするのに必要なエネルギーです。
イオン化エネルギー
1molの原子から電子を奪い陽イオンにするのに必要なエネルギーです。エンタルピーの計算方法
反応エンタルピーのうち,生成エンタルピーと燃焼エンタルピーを用いることでほかの反応エンタルピーを計算することができます。また結合エネルギーや解離エネルギーを用いて反応エンタルピーを求めることもできます。
生成エンタルピーを用いた求め方
これまでと同じ,3つの反応エンタルピーを付した化学反応式(冗長なので以下,熱化学反応式とします)を用います。
C(黒鉛) + 2H2(気) + \(\frac 12\)O2(気) → CH3OH(液) \(\Delta H_1 = -239kJ/mol\) ‥‥‥①
C(黒鉛) + O2(気) → CO2(気) \(\Delta H_2 = -394kJ/mol\) ‥‥‥②
H2(気) + \(\frac 12\)O2(気) → H2O(液) \(\Delta H_3 = -286kJ/mol\) ‥‥‥③
これら3式を持ちてメタノールの燃焼エンタルピーを求めてみます。メタノール燃焼の化学反応式は次の通り
CH3OH(気) + \(\frac 32\)O2(気) → CO2(気) + 2H2O(液) ‥‥‥④
ここで④式の生成物の反応エンタルピーと反応物の生成エンタルピーの総和の差をとることで燃焼エンタルピーを求めます。酸素O2の生成エンタルピーは0kJ/molであることに注意してください。
\(Delta H=\)《生成物の生成エンタルピーの総和》《反応物の生成エンタルピーの総和》$$=(-394-286 \times 2 ) – (-239 – \frac 32 \times 0)=-727kJ/mol$$
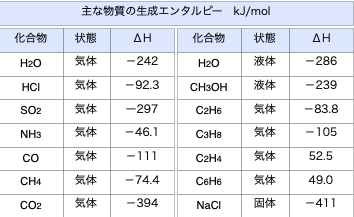
となります。単位がkJではなくkJ/molとなっているのは燃焼エンタルピーの定義が「1molの物質を燃焼させたときの反応エンタルピー」となっているからです。主な化合物の生成エンタルピーは次のような値です。これらの値を用いることで様々な反応の反応エンタルピーを求めることができます。
《生成物の生成エンタルピーの総和》《反応物の生成エンタルピーの総和》
上記の数値を用いてプロパンの燃焼エンタルピーを求めてみると
C3H8(気) + 5O2(気) → 3CO2(気) + 4H2O(液)
$$\Delta H = (-394 \times 3 -286 \times 4 )-(-105-0\times 5)=-2221kJ/mol$$
のようになります
燃焼エンタルピーを用いた求め方
生成エンタルピーを用いた方法と同様に
《反応物の燃焼エンタルピーの総和》《生成物の燃焼エンタルピーの総和》
という公式で反応エンタルピーを求めることができます。メタノールの生成エンタルピーを黒鉛,水素,メタノールの燃焼エンタルピーで求めてみます。
黒鉛,水素,メタノールの燃焼エンタルピーはそれぞれ ,
,
とします。メタノールの生成反応は次のように表されます。
C(黒鉛) + 2H2(気) + \(\frac 12\)O2(気) → CH3OH(液)
上の公式を適用して$$\Delta H = (-394 -286 \times 2 + \frac 12 \times 0)-(-727)=-239kJ/mol$$
となります。主な物質の燃焼エンタルピーは次のような値になっています。
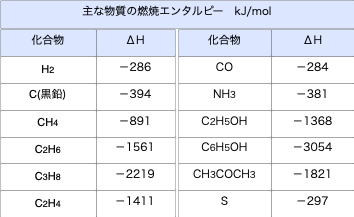
結合エネルギーを用いた反応エンタルピーの求め方
主な結合の結合エネルギーは次の表のようになっています。
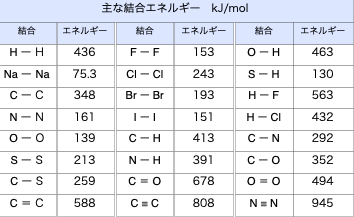
この表の値を用いて反応エンタルピーを求めるには
《反応物の結合エネルギーの総和》《生成物の結合エネルギーの総和》
の公式を使います。
C2H4(気) + H2(気) → C2H6(気) ‥‥‥①
の反応エンタルピーは$$\Delta H = (588 + 436)-(348-413 \times 2)=-150kJ$$
となります。エチレンの二重結合()と水素分子の共有結合(
)を切り,必要な箇所を繋ぎ合わせます(
)。
エントロピーと反応の自発性
ここまでは旧課程と新課程の違いを見てきました。ざっくり言うと
「反応熱・熱化学方程式」の表記を「エンタルピー」を用いた表記に変えた
だけでした。符号が変わるなど,混乱させられそうな要因はありますが,新しいことはなかったように思います。
ここからは新しい概念を説明します。物質の乱雑さ,エントロピーです。
エントロピーの概念を,氷の融解の反応を例に説明します。氷の融解エンタルピーは6.0kJ/molで反応エンタルピーを付した化学反応式は
H2O(固) → H2O(液) \(\Delta H = 6.0kJ/mol\)
となります。\(\Delta H>0\)だから氷の融解は吸熱反応です。
氷を室内に置いておくと溶けていきますが,エンタルピーが増加するこの反応がなぜ自発的に起こるのか‥‥これを説明するのに必要な概念がエントロピーです。
一般に物質は安定になろうとします。水は低いほうに流れるようなものと思ってください。これをエンタルピーで説明すると,エンタルピーは少なくなろうとする‥‥ということになります。ところがこの理屈でいくと自発的に起こる化学反応の反応エンタルピーは必ず負の値になってしまいます。しかし実際には上記の氷の融解のように反応エンタルピーが正の,吸熱反応の中にも自発的に起こる反応があります。この事実を説明するための概念がエントロピーです。
実は、物質は安定になろうとする性質以外に,乱雑さを増やそうとする性質を持っています。整理された部屋も徐々に散らかっていく‥‥ようなものだと思ってください。吸熱反応である氷の融解が自発的に起こるのは,安定になろうとすること(エンタルピーを減少させる)よりも乱雑さを増やそうとする(エントロピーを増加させる)性質が上回ったから‥‥と説明されます。
他にも例をあげます。空気の主成分は酸素と窒素です。分子量を考えると酸素の方が少し重い‥‥では空気は地面に近いほど酸素の比率が高い‥‥ということはありません。地表付近の空気中の酸素,窒素の比率はどこでも同じ,均一に混ざっています。安定になろうとする性質よりも乱雑になろうとする性質が上回っているため,空気は乱雑に(すなわち均一に)なっています。この乱雑さを表す量がエントロピーです。
物質のエントロピーは増大しようとする性質を持っています。化学反応が自発的に起こるかどうかはエンタルピーの変化量とエントロピーの変化量の2つの要因により決定されます。
ギブズエネルギー(参考)
反応エンタルピー\(\Delta H\)とエントロピー変化\(\Delta S\)の2つの値と絶対温度T[K]を用いて定義される次の値\(\Delta G\)をギブスエネルギーと言います。$$\Delta G = \Delta H -T \Delta S$$
このギブスエネルギーを用いると化学反応が自発的に進むかどうかが判断できます。すなわち,\(\Delta G < 0\) のとき反応は自発的に進み\(\Delta G > 0\)のとき,逆反応が自発的に進みます。先の氷の融解について,温度が 0℃(273K)のときののギブスエネルギーの値は\(\Delta G = 0\)となっており,0℃のとき氷の融解は進みません。温度が高いと\(\Delta G < 0\)となり氷は溶け,温度が0℃よりも低くなると\(\Delta G > 0\)となり水が氷に変わります。
以上です。電子書籍版には例題・資料なども掲載しています。


コメントを残す